For many population genetic analyses, we simulate genetic data under different evolutionary histories (different data models) to then assess which model fits best to the observed data, and thus which evolutionary history explains the data best. As genomic data of any individual is inherited from ancestors and changed by recombination and mutation, an efficient way to formulate these data models is to model the ancestral relationships and how mutation and recombination work alongside these. These ancestry models are called coalescent models (for a single locus) or ancestral recombination graphs (genome-wide), see Nielsen et al. (2025).
Inference machineries based on these models work well if the models reflect the underlying genetical constraints for the analysed species. A crucial factor for designing a well-fitting ancestry model is accounting for the mode of reproduction (haploid, diploid, inbreeding, selfing etc.), especially if offspring sizes can be very large, e.g., Nordborg and Donnelly (1997), Birkner et al (2018). A significant proportion of animal and fungal species have a reproduction mode between haploid and diploid: some offspring inherit genomic information from two parents and some from only one, while potentially featuring large variation in offspring numbers (Figure 1 shows a simplified model). Mathematical models for reproduction and forward-in-time evolution exist, see Billiard and Tran (2012), Tezenas et al. (2023), Tyvand and Thorvaldsen (2010) and Pracana et al. (2022), but a mathematical description of the associated ancestry models is missing.
You will design such an ancestry model, e.g. for haplodiploid reproduction in social insects. You will derive its mathematical properties, develop a bioinformatic simulation approach and assess its fit to real genomic data.
This project aims to improve a crucial tool to analyse the genomic properties of many key species: 15% of animal species are haplodiploid (Pracana et al., 2022), involved in economically and environmentally crucial processes as pollination, seed dispersal and soil turnover. This improvement will allow us to better understand and predict how species thrive or struggle in current or changing environments.
As this project is in between mathematics, bioinformatics and genetics, you will develop and learn a diverse range of skills.
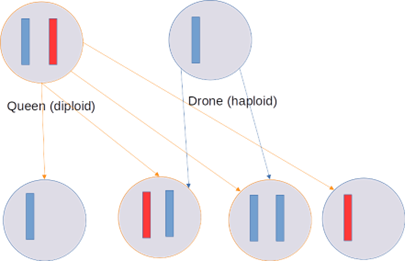
Figure 1: Simplified chromosome haplodiploid reproduction scheme for insects according to Tyvand and Thorvaldsen (2010). Queens produce eggs with one random chromosome copy (rectangles) of their 2 chromosomes, which become haploid drones if not fertilized, or receive a 2nd chromosome copy from a haploid drone.
This project is not suitable for CASE funding
Each host has a slightly different application process.
Find out how to apply for this studentship.
All applications must include the CENTA application form.
Choose your application route
You will establish a forwards-in-time probabilistic reproduction model based on properties of existing species with mixed reproduction modes (haplodiploidy, cycles of sexual and clonal reproduction), You will then mathematically derive the corresponding genealogical process of a sample, likely as a large population size limit. For this, we can draw from the population genetics literature which provides several approaches to derive such limits. Then, its mathematical properties can be further analysed, e.g. establishing the distribution of tree properties as the time to the most recent common ancestor of the sample or genetic diversity statistics as the site frequency spectrum under this model.
On the bioinformatic side, you will implement this model in R or Python – e.g. within the framework of the Python package msprime. You will then simulate genetic diversity statistics under this model and assess whether real samples from appropriate species indeed are showing values as generated under this model.
DRs will be awarded CENTA Training Credits (CTCs) for participation in CENTA-provided and ‘free choice’ external training. One CTC can be earned per 3 hours training, and DRs must accrue 100 CTCs across the three and a half years of their PhD.
Apart from the direct in-group training in population genetics, reproductive modes, coalescent theory and bioinformatics, you will be encouraged and enabled to participate in summer schools, external PhD training courses (e.g., EMBO courses), conferences (e.g., popgroup meeting) and we will work towards a research visit in a lab of collaborators either in UK or abroad (central Europe).
Year 1: Formulating forwards-in-time reproduction models, assessing coalescent theory usable here, start deriving ancestral processes.
Year 2: Mathematically deriving ancestral process, adding mutational processes, coding simulation approach of both, genomic data collection to assess fit of model to (publicly available, in-house or from partner labs, already sequenced and aligned)
Year 3: Fitting model to collected data, refining model, adding features (recombination, demographic changes) to make more realistic
Billiard, Sylvain, and Viet Chi Tran. 2012. “A General Stochastic Model for Sporophytic Self-Incompatibility.” Journal of Mathematical Biology 64 (1): 163–210.
Birkner, Matthias, Huili Liu, and Anja Sturm. 2018. “Coalescent Results for Diploid Exchangeable Population Models.”
Nielsen, Rasmus, Andrew H Vaughn, and Yun Deng. 2025. “Inference and Applications of Ancestral Recombination Graphs.” Nature Reviews Genetics 26 (1): 47–58.
Nordborg, Magnus, and Peter Donnelly. 1997. “The Coalescent Process with Selfing.” Genetics 146 (3): 1185–95.
Pracana, R., Burns, R., Hammond, R.L., Haller, B.C. and Wurm, Y., 2022. Individual-based modeling of genome evolution in haplodiploid organisms. Genome Biology and Evolution, 14(5), p.evac062.
Tezenas, Emilie, Tatiana Giraud, Amandine Véber, and Sylvain Billiard. 2023. “The Fate of Recessive Deleterious or Overdominant Mutations Near Mating-Type Loci Under Partial Selfing.” Peer Community Journal 3.
Tyvand, Peder A, and Steinar Thorvaldsen. 2010. “Wright–Fisher Model of Social Insects with Haploid Males and Diploid Females.” Journal of Theoretical Biology 266 (3): 470–78.
For any enquiries related to this project please contact Dr. Fabian Freund, University of Leicester, [email protected].
To apply to this project:
Applications must be submitted by 23:59 GMT on Wednesday 7th January 2026.